資料探索的檢定_主成分分析, 多變量變異數分析, 集群分析_R語言

發布時間：2018年8月28日

資料型態: 幾乎任何資料都可以拿來做資料探索，實務上，當變數數目跟觀測數都夠多時，資料探索的用處比較大。資料探索的目的為處理觀測值之間的交互關係，並將期間模式凸顯給實驗者。

主成分分析和因素分析 (Principle component analysis (PCA) and factor analysis)

都是藉由加權變數來將每個個體的差異最大化。許多方面，主成分分析跟相關係數和回歸分析很類似。只要資料中每個個體都有兩個以上的觀測值就可使用。主成分分析假第資料是連續的且遵從常態分佈。若執行此分析的目的是為了建立新假設就可以忽略此假定。

視覺化:

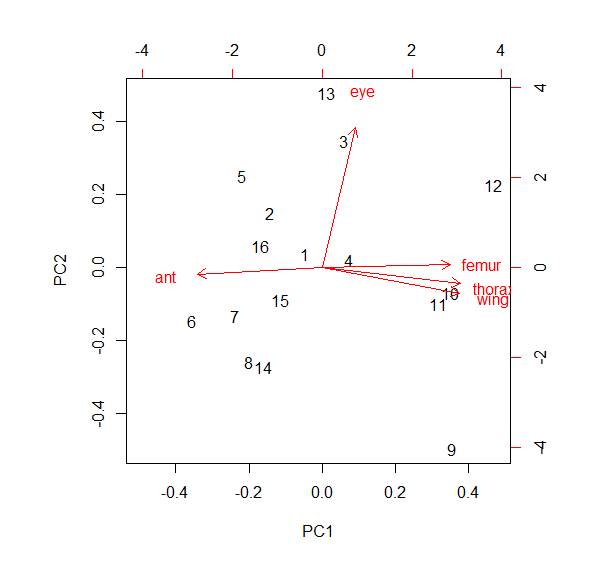
藉由「每個個體指有兩個觀測值」的特例將主成分分析的運作視覺化。想像將兩個相關的變數製成散佈圖，其資料形成橢圓形雲狀物。PCA會計算通過此橢圓形長軸的直線，並將此直線當成第一個主要軸線(PCA1)。通過資料雲，且和第一個軸線垂直的直線就是PCA2。分析過程是電腦以多維空間的形式進行，每個變數都代表一個維度，每條通過資料雲的直線都來自對於個變數做適當的加權。

PCA主成分分析原理及分析實踐詳細介紹 (很詳盡的介紹，也有R的演示)

Example: 研究兩種果蠅物種，觀察資料包含五種型態的單位、性別和物種別。

R
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

sex<- c(1,1,1,1,2,2,2,2,1,1,1,1,2,2,2,2)
species<- c(1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2)
thorax<- c(1.01,0.98,1.02,1.05,0.98,0.89,0.89,0.95,1.20,1.15,1.18,1.21,0.95,0.94,0.96,0.91) #胸長
wing<- c(2.51, 2.45, 2.57, 2.61, 2.40,2.35, 2.38,2.41,3.10,3.12, 3.21, 3.20, 2.51,2.50,2.62,2.45) #翅長
femur<- c(.06,.05,.08,.07,.04,.04,.05,.05,.09,.10,.09,.10,.08,.07,.08,.07) #腿長
eye<- c(.52,.53,.55,.52,.54,.50,.50,.49,.48,.52,.52,.55,.56,.49,.51,.52) #眼距
ant<- c(.11,.12,.11,.10,.13,.14,.12,.12,.09,.10,.11,.09,.11,.13,.14,.13) #第三節觸角
data.frame(sex,species,thorax,wing,femur,eye,ant)
summary(prcomp(~thorax+wing+femur+eye+ant, scale= T)) #以prcomp()或princomp()皆可執行，結果也很相似，再來是定義主成分分析的變數(thorax, wing,femur, eye, ant)，但是分組變數不能輸入(species, sex)主成分分析中，最後加上「scale=T」讓個效果總合等於1。
#輸出結果顯示各主成分解釋多少比例的變異數: 「PCA1」解釋68.4%; 「PCA2」解釋19.8%

Importance of components:
 PC1 PC2 PC3 PC4 PC5
Standard deviation 1.8491 0.9941 0.61878 0.43913 0.12914
Proportion of Variance 0.6839 0.1976 0.07658 0.03857 0.00334
Cumulative Proportion 0.6839 0.8815 0.95810 0.99666 1.00000
print(prcomp(~thorax+wing+femur+eye+ant, scale= T)) #顯示各主成分中各變數項目的權重

Standard deviations (1, .., p=5):
[1] 1.8491400 0.9941184 0.6187849 0.4391321 0.1291438

Rotation (n x k) = (5 x 5):
 PC1 PC2 PC3 PC4 PC5
thorax 0.5185966 -0.11303213 0.1408875 -0.5248445 0.65036167
wing 0.5150173 -0.17934884 -0.2514674 -0.3870185 -0.69969423
femur 0.4818698 0.01774549 -0.5946408 0.6000820 0.23192783
eye 0.1236216 0.97599696 -0.0548311 -0.1635158 -0.04902823
ant -0.4672622 -0.04661295 -0.7485390 -0.4334964 0.17681459

#第一個主成分(PCA1)給予前四項變數正向的權重；ant則是負向權重。第二個主成分(PCA2)的權重顯示eye是最重要的。
biplot(prcomp(~thorax+wing+femur+eye+ant, scale= T)) #視覺化

PCA.png

典型變量分析 (Canonical variate analysis):

與PCA的運作模式大致相同，執行該分析前必須把所有個體分組。其算出的變相權重是極大化的各組差異，而非PCA的個體差異。其產生的變數權重可以判斷哪些變數差異最大，那些無差異。進行本分析時盡量使用有現實意義的分組而非人為分組。

區別函數分析 (Discriminant function analysis):

和典型變量分析一樣需先將個體分組。該分析的想法是先計算出能夠分辨各組的權重，並把這組權重套用到尚未被分組的個體，以求得這些個體屬於個別組的機率。

R
1
2
3
4
5
6
7

install.packages(MASS)
library(MASS)
fit<- lda(species~thorax+wing+femur+eye+ant, CV=T) #將species定義為辨別目標
fit #輸出結果中，「$class」給出各個體的分組狀況。「$posterior」給出各個體分屬各組的機率。如第一個個體有0.99.92被分配到品種1
ct<- table(species, fit$class)
diag(prop.table(ct,1))#顯示各品種被正確分配的機率
sum(diag(prop.table(ct))) #總分組正確率

多變量變異數分析 (Multivariate analysis of variance) (MANOVA)

R
1
2
3
4
5

y<- cbind(thorax,wing) #合併兩個應變數
fit<- manova(y~species) 
summary.aov(fit) #以單變量分析結果顯示thorax和物種關係不顯著，wing則顯著
summary.aov(fit,test= wilks) #指定以Wilks版本做多變量分析，具有顯著差異。其他版本還有Roy和Pillai，結果大同小異。
summary(fit, test= Wilks)

多變量共變數分析 (Multivariate analysis of covariance) (MANCOVA):

如果有大於一個觀測項目，一個以上分組方法，且已經有另一個變數會影響觀測項目，則可以使用該分析移除干擾變數。

集群分析 (Cluster analysis):

一群個體分類法的統稱。隨著對DNA序列分析對統計的需求越來越精細，這些方法也越來越重要。集群分析可以畫出樹狀圖親緣關係，藉以顯示可能的親緣關係，或至少把各個體分成數個可能有分類學意義的組別。集群分析應用範圍不只限於分子序列分析。除了分類學領域也可以應用於集群生態學，近年來更成為研究基因表現和基因家族的關鍵方法。

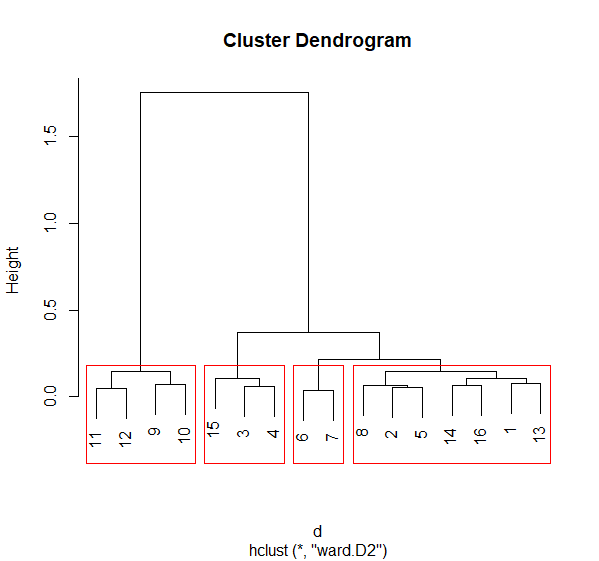
最單純的集群分析可視為一種按部就班的迴圈過程。先將

  1. 各個體資料轉化為散佈的資料點
  2. 找尋最相近的兩個個體，將其相似度紀錄為兩點的距離
  3. 將這兩點合併成一點，位置取在兩點正中間
  4. 再去找最近的兩點合併，不斷重複直到剩下一個點。
R
1
2
3
4
5
6

y<- cbind(thorax,wing,eye,femur,ant) #將要用到的變數綁定到同一件
d<- dist(y, method = euclidean) #dist()求出各個體的[歐幾里得距離](https://zh.wikipedia.org/wiki/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E8%B7%9D%E7%A6%BB)，並存在d
fit<- hclust(d, method = ward.D2) #hclust()執行階層集群分析，使用方法為Waed
plot(fit) #匯出樹狀圖
groups<- cutree(fit, k=4)
rect.hclust(fit, k=4, border = red) #添加四個紅色框框分群

cluster.png

降趨勢對應分析(DECORANA)和雙向指標物種分析 (TWINSPAN):

為當今族群的物種豐富度資料分析和生態資料的分析均廣為使用本方法 目前尚未更新，似乎需要在3.5.0版本才能使用

R
1
2
3
4
5

data(varespec)
vare.dca <- decorana(varespec)
vare.dca
summary(vare.dca)
plot(vare.dca)

參考來源: 生物統計學：如何選擇與應用

相關文章