在 R 執行 SAS 的 glm lsmeans
使用的資料為 R 內建的 dataset- airquality
可以先看一下該資料的描述(紐約某一年的空氣品質指標數據)
?airquality
head(airquality)輸出為 csv 檔供 SAS 使用
airquality$Month<- as.factor(airquality$Month)
write.csv(airquality, file = airquality.csv)假設我們的實驗目的是要比較各月份的溫度是否有差異
建立線性模型
formula 用於將 Temp(反應變數)迴歸於 Month(預測變數),使用的資料為 airquality
day 為類別變數# 把-1 放在 formula 裏是不要讓截距項涵蓋在模型裏;
類別變數將自動地被設定成每個 level 都會有一個迴歸係數
Temp_lm<- lm(Temp~ Month -1 , data= airquality)
Temp_lm #結果顯示Intercept(截距項)和Month各類別的係數
Call:
lm(formula = Temp ~ Month - 1, data = airquality)
Coefficients:
Month5 Month6 Month7 Month8 Month9
65.55 79.10 83.90 83.97 76.90
summary(Temp_lm)
#summary顯示更多模型的結果,其中包括標準誤差(Std.Error)、t 檢定值(t value)、針對回歸係數的 p 值(Pr(>|t|))、自由度(degrees of freedom)、殘差(Residual)的摘要統計和F檢定結果
Call:
lm(formula = Temp ~ Month - 1, data = airquality)
Residuals:
Min 1Q Median 3Q Max
-14.100 -4.548 -0.900 3.900 16.100
Coefficients:
Estimate Std. Error t value Pr(>|t|)
Month5 65.548 1.195 54.83 <2e-16 ***
Month6 79.100 1.215 65.09 <2e-16 ***
Month7 83.903 1.195 70.19 <2e-16 ***
Month8 83.968 1.195 70.24 <2e-16 ***
Month9 76.900 1.215 63.28 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.656 on 148 degrees of freedom
Multiple R-squared: 0.993, Adjusted R-squared: 0.9928
F-statistic: 4221 on 5 and 148 DF, p-value: < 2.2e-16其實會 ANOVA 和回歸結果都是一樣的線性模型推導出來的
執行 lsmenas 比較每個月溫度是否有差異
安裝執行 lsmeans 所需套件
install.packages(emmeans)
library(emmeans)
Temp_lsm<- lsmeans(Temp_lm, Month)
Temp_lsm
Month lsmean SE df lower.CL upper.CL
5 65.54839 1.195454 148 63.18602 67.91075
6 79.10000 1.215215 148 76.69859 81.50141
7 83.90323 1.195454 148 81.54086 86.26559
8 83.96774 1.195454 148 81.60538 86.33010
9 76.90000 1.215215 148 74.49859 79.30141
Confidence level used: 0.95以 contrast 函數執行兩兩比較各月份溫度差異,引數的interaction= T
contrast(Temp_lsm, method = pairwise, interaction = T)
Month_pairwise estimate SE df t.ratio p.value
5 - 6 -13.55161290 1.704657 148 -7.950 <.0001
5 - 7 -18.35483871 1.690627 148 -10.857 <.0001
5 - 8 -18.41935484 1.690627 148 -10.895 <.0001
5 - 9 -11.35161290 1.704657 148 -6.659 <.0001
6 - 7 -4.80322581 1.704657 148 -2.818 0.0055
6 - 8 -4.86774194 1.704657 148 -2.856 0.0049
6 - 9 2.20000000 1.718573 148 1.280 0.2025
7 - 8 -0.06451613 1.690627 148 -0.038 0.9696
7 - 9 7.00322581 1.704657 148 4.108 0.0001
8 - 9 7.06774194 1.704657 148 4.146 0.0001將 Temp_lm 製成圖表
library(plyr)
library(ggplot2)
TempInfo<- summary(Temp_lm)
TempCoef <- as.data.frame(TempInfo$coefficients[, 1:2])
TempCoef <- within(TempCoef, {
Lower <- Estimate - qt(p=0.90, df=TempInfo$df[2]) * `Std. Error`
Upper <- Estimate + qt(p=0.90, df=TempInfo$df[2]) * `Std. Error`
Month <- rownames(TempCoef)
})
ggplot(TempCoef, aes(x=Estimate, y=Month)) + geom_point() +
geom_errorbarh(aes(xmin=Lower, xmax=Upper), height=.3) +
ggtitle(Temp by Month calculated from regression model)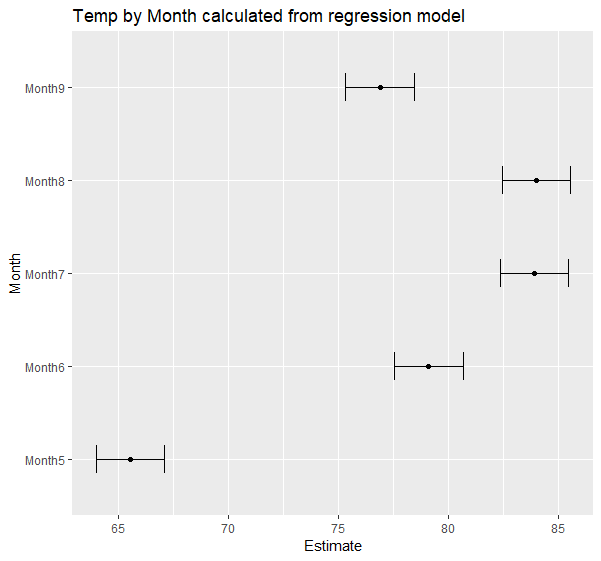
現在換成在 SAS 中執行 glm 中的 lsmeans 語法
PROC IMPORT
DATAFILE= C:\\R\\airquality.csv /* 要匯入資料的資料位置 */
OUT= Course.airquality /* 儲存到SAS的哪個位置*/
DBMS= CSV /* 匯入檔案的格式*/
REPLACE; /*宣告匯入的資料覆寫現有的資料集,系統預設是不覆寫,如不宣告則可能導致匯入資料重複*/
GETNAMES=YES; /*宣告是否將資料的第一行當作變項名稱*/
run;
/*匯入資料方式的參考來源 https://blog.timshan.idv.tw/2013/06/howtoimportsas.html */
proc print data = Course.airquality;
run;
proc glm data = Course.airquality;
class Month;
model Temp = Month ;
lsmeans Month/ stderr pdiff;
run;下面這個網誌簡單的說明 lsmeans 的功能,使各組間 means 的權重一致,達到修正模型的結果
[SAS] 多重比較 based on “Least Squares Means (lsmeans)
SAS 得到的結果如下
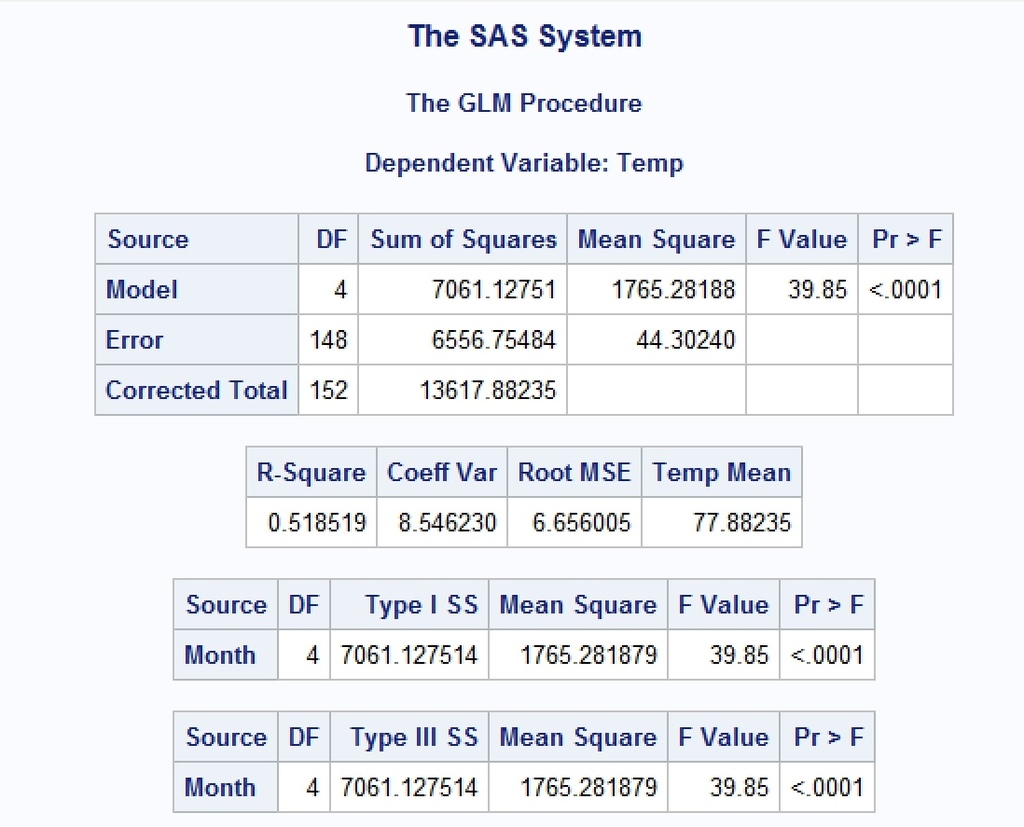
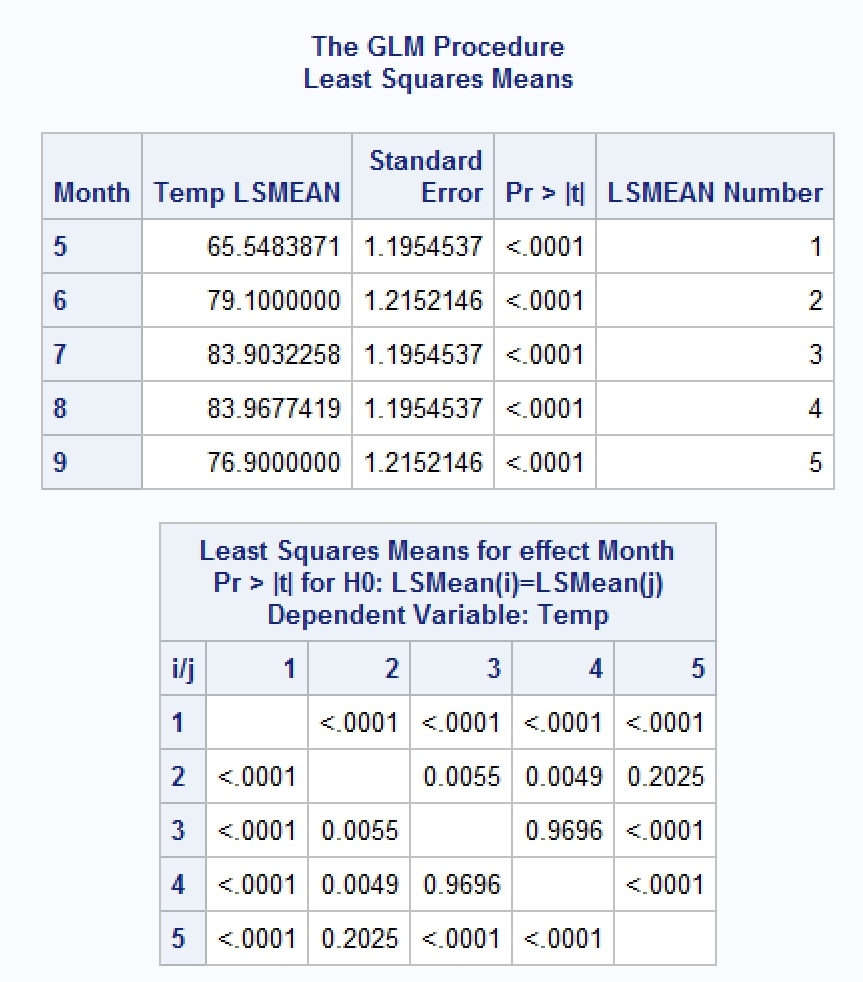
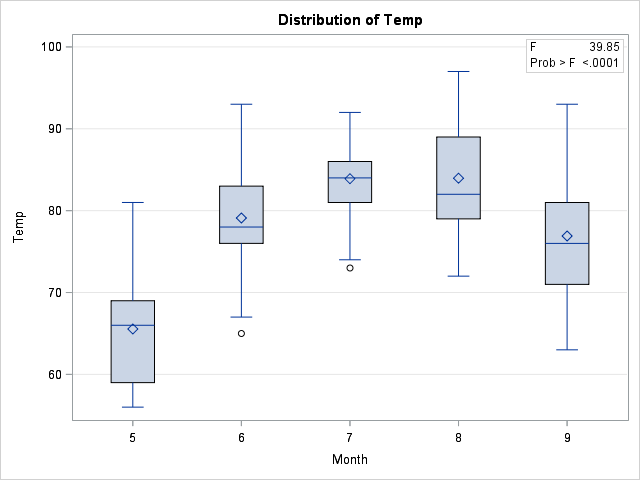
後記: 其實我是在先學 SAS 的 glm 語法,所以一直以為這種統計方法是 glm(廣義線性回歸模型)
後來才發現這只是 SAS 的語法名稱而已,實際上的統計方式還是簡單線性回歸模型而已
想說明明比較的只有各類別中的數值而已,怎麼會需要用到 glm

